Tweet

Operações Básicas com Números Complexos

Neste artigo vamos estudar as operações aritméticas básicas com números complexos: adição, subtração, conjugado, multiplicação e divisão.

1 – Adição de Números Complexos

Para somar dois números complexos devemos adicionar cada parte separadamente, conforme o padrão:

(a+bi) + (c+di) = (a+c) + (b+d)i

Exemplo:

Adicionar 4 + 2i e 1 + 9i:

(4 + 2i) + (1 + 9i) =
4 + 1 + (2 + 9)i = 
5 + 11i

2 – Multiplicação de Números Complexos

Cada parte do primeiro número complexo é multiplicada por cada parte do segundo número complexo, desta forma:

(a+bi)(c+di) = ac + adi + bci + bdi2

Exemplo:

(2 + 3i)x(1 + 8i) = 
2x1 + 2x8i + 3ix1 + 3ix8i = 
2 + 16i + 3i + 24i2 = 
2 + 16i + 3i -24 (i2 = -1) = 
-22 + 19i

3 – Subtração de Números Complexos

Para subtrair um número complexo de outro, subtraímos cada parte separadamente:

(a+bi) - (c+di) = (a-c) + (b-d)i

Exemplo: Efetuar (3 + 5i) – (1 + 3i):

(3 + 5i) - (1 + 3i) =
3 - 1 + (5 - 3)i = 
2 + 2i

4 – Obter o conjugado de um número complexo

O conjugado de um número complexo nada mais é do que o número com o sinal trocado em sua parte imaginária. Por exemplo, o conjugado de 2 + 7i é 2 – 7i.

O conjugado é empregado, por exemplo, para auxiliar na operação de divisão entre números complexos, como veremos a seguir.

5 – Divisão de Números Complexos

A divisão de complexos é um processo ligeiramente mais “complexo”. Por exemplo, vamos dividir o complexo 5 + 2i por 7 + 4i:

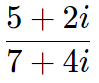
1. O primeiro passo é determinar o conjugado do denominador:
Conjugado de 7 + 4i = 7 -4i

2. Multiplicamos o numerador e o denominador pelo conjugado do denominador:

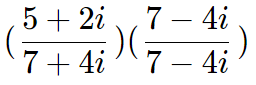
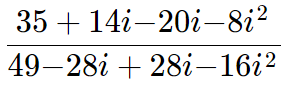Devemos lembrar que i² = -1: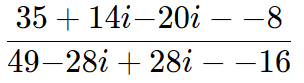Finalmente, juntamos os termos semelhantes e simplificamos: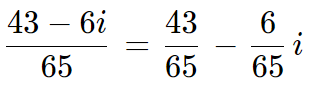

É isso aí! No próximo artigo mostraremos como plotar números complexos em um gráfico no plano cartesiano. Até!

Referências

Laforest, M. The Mathematics of Quantum Mechanics. University of Waterloo. 2015.