Tweet

Introdução ao Números complexos

Os números, tais como conhecemos e usamos no dia-a-dia, incluindo valores como 15, -25, 0,67, √6, 97/13 e π, são conhecidos como números reais. Denotamos a família de números reais com o símbolo ℝ.

Uma característica dos números reais é de que quando um número real é elevado ao quadrado sempre obtemos um resultado positivo, independente do número em si ser positivo ou negativo. Assim, 5² = 25 e -5² = 25 também.

Em algumas circunstâncias, precisamos fazer cálculos para os quais os números reais não são suficientes – por exemplo, o cálculo pode ser extremamente complicado de se realizar, o até mesmo impossível.

Um exemplo clássico e banal é o cálculo das raízes de uma equação do segundo grau, na forma ax²+bx+c = 0, que é resolvida com a seguinte fórmula:

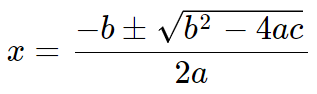
O problema é que, às vezes, o valor de b²-4ac é um número negativo, e precisamos calcular a raiz quadrada desse número na fórmula. Mas, como calcular raízes de números negativos? No domínio dos números reais isso é impossível.

Isso significa então que esse tipo de equação pode não ter solução? Não. Na verdade, é possível resolver a equação, mesmo com raízes de números negativos – desde que usemos o conceito de números complexos.

O que é um número complexo

Para entendermos o que é um número complexo vamos realizar algumas definições.

Números imaginários: são números que, ao serem elevados ao quadrado, retornam um resultado negativo..

Por exemplo: o valor 

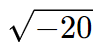
é imaginário porque, ao ser elevado ao quadrado, retorna o valor -20.

Número unitário imaginário: Definimos o número unitário imaginário i como sendo a raiz quadrada de -1, ou seja:

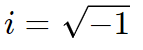
Isso significa que se elevarmos i ao quadrado, obteremos o valor -1, ou seja:

i² = -1

Exemplos de números imaginários:

• 3i
• 3,4i
• 4i/5
• -63i
• (√5)i

Números Complexos: Um número complexo z é uma combinação de um número real com um número imaginário, escrito no formato:

z = a + bi

onde a é a parte real do número, e bi é a parte imaginária (b é um número real), representadas por Re() e Im(), como segue:

Re(z) = a
Im(z) = bi

Exemplos de números complexos:

• 2 + i
• 22 + 3i
• 3,4 – 6i
• -5 + 0,5i
• 0 + 12i

Na prática, um número real nada mais é que um número complexo, porém sem sua parte imaginária. Denotamos o conjunto dos números complexos por ℂ e, assim, podemos dizer que:

ℝ ⊂ ℂ

que significa: “ℝ está contido em ℂ“

Da mesma forma, um número imaginário é um número complexo, porém sem sua parte real.

Aplicações dos números complexos

Os números complexos encontram diversas aplicações, em inúmeras áreas, tais como:

• Eletromagnetismo
• Mecânica quântica
• Processamento de sinais
• Cartografia
• Geometria
• Química
• Cálculo de Circuitos Elétricos

e muitas outras.

Exemplo

Vamos resolver a equação de segundo grau (quadrática) x² + 5x + 10 = 0.

Resolução:

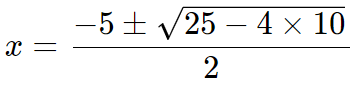
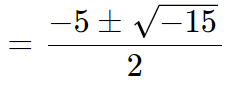
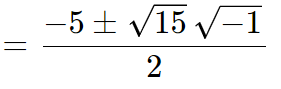
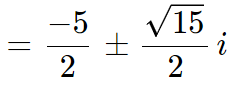
Como pudemos ver, mesmo nos deparando com uma raiz de número negativo na equação (raiz de -15), foi possível resolver o problema no domínio dos números complexos.

Na próxima lição vamos apresentar diversas operações aritméticas que podem ser realizadas com os números complexos, tais como soma, multiplicação e divisão, entre outras.

Referências

Laforest, M. The Mathematics of Quantum Mechanics. University of Waterloo. 2015.