O que é Notação Big O em programação e análise de algoritmos
Notação Big O
A notação Big O é um conceito matemático normalmente empregado para medir o custo de um algoritmo. É uma forma simples de classificar a complexidade computacional de um algoritmo.
No geral, significa encontrar uma função que relacione o tamanho da entrada de um algoritmo com o número de passos necessários à sua execução (complexidade temporal) ou quantidade de espaço de armazenamento que ele emprega (complexidade espacial).
Comumente a função que descreve a performance de um algoritmo se refere ao seu limite superior, que determina o pior caso (de entrada de dados) do algoritmo.
Em ciência da computação, a notação Big O é empregada para classificar algoritmos de acordo com seu tempo de execução / número de passos (custo) ou requisitos de espaço, conforme a entrada de dados aumenta.
|
Análise de Algoritmos, termo cunhado pelo cientista da computação Donald Knuth (autor de The Art of Computer Programming), é o processo de encontrar a complexidade computacional de um algoritmo. Complexidade computacional se refere à quantidade de tempo, armazenamento ou outros recursos necessários para a execução de um algoritmo. |
Em outras palavras, usamos essa notação para indicar quanto tempo algo demorará para executar, ou o espaço que ocupará na memória, dado uma quantidade N de dados a serem manipulados.
Qual a importância de saber isso? Vai te permitir desenvolver software muito melhor porque você irá entender como é possível melhorar a performance do programa, tornando-o mais eficiente e escalável, sem complexidade adicional.
Se um projeto precisa usar um algoritmo específico, é importante entender o quão rápido ou lento ele é em comparação com outras alternativas.
Definição Formal de Big O
A seguir temos uma definição formal da notação Big O, retirada da Wikipedia:
“A notação Big O é uma notação matemática que descreve comportamento limite de uma função quando o argumento tende a um valor em particular ou ao infinito.”
Trata-se de uma notação membro de uma família de notações inventadas por Paul Bachmann, Edmund Landau e outros, chamadas em conjunto de Notação Bachmann-Landau ou ainda Notação Assintótica.
Curiosidade: A letra ‘O’ vem da palavra em alemão Ordnung, com o significado de Ordem (de aproximação).
O Big O se foca no cenário de pior caso no qual o algoritmo consome o maior tempo (ou recursos) para executar. Isso significa que o algoritmo nunca irá demorar MAIS que esse cenário – mas pode demorar MENOS em determinadas circunstâncias.
Perceba que essa notação serve para calcular o tempo máximo que irá demorar a execução do algoritmo (em termos de custo), mas o tempo real pode ser menor. Por exemplo, uma busca linear em um array pode encontrar o item na primeira posição pesquisada, como se fosse O(1) (melhor resultado).
Assim, o Big O sempre se refere ao pior resultado possível.
Note que o Big O serve para algoritmos escritos em qualquer linguagem de programação e sempre é calculado da mesma forma.
Observação importante: essa notação NÃO nos informa a velocidade de um algoritmo em segundos, pois existem muitos fatores que podem influenciar essa velocidade, como por exemplo o hardware empregado para executar o algoritmo. Usamos o Big O para comparar algoritmos entre si.
Funções e Complexidade
Na notação Big O, a letra “n” representa o tamanho da entrada, enquanto a função “g(n) = n”, associada ao “O()” nos informa a complexidade do algoritmo em relação ao tamanho dessa entrada.
Sendo assim, podemos ter algoritmos classificados de acordo com seu nível de complexidade, como segue:
- Complexidade Constante: O(1)
Não importa a quantidade total de dados acessados, o tempo de acesso é sempre 1, ou seja, sempre o mesmo custo para acessar qualquer um dos dados no conjunto. Exemplo: acesso a um elemento de um array. - Complexidade Linear: O(n)
O acesso a um elemento demora o tempo equivalente à quantidade de dados da coleção. Exemplo: busca linear de um dado em uma lista ou array não ordenado – o algoritmo, no pior caso, tem de procurar em até n elementos, caso o dado buscado ser o último ou inexistente. - Complexidade Logarítmica O(log n)
Sua performance aumenta drasticamente conforme a quantidade de elementos aumenta. Exemplo: árvores de busca balanceada ou algoritmos de busca binária em arrays. Sua performance se aproxima comumente do O(1).
Geralmente os dados precisam estar classificados (ordenados) de alguma forma. - Complexidade Linearítmica: O(n log n)
É uma combinação das complexidades linear e logarítmica. Algoritmos que usam estratégias do tipo dividir e conquistar são linearítmicos, como os algoritmos de classificação Merge Sort e Heap Sort. - Complexidade quadrática O(n2)
Complexidade na qual o custo computacional cresce de acordo com o quadrado da quantidade de elementos de entrada. Exemplo de algoritmo: Algoritmos de classificação como Bubble Sort, Insertion Sort ou Selection Sort. - Complexidade polinomial (nc)
A quantidade de operações é proporcional à potência c do tamanho da entrada (engrada elevada a um valor c).
Exemplo: Encontrar o determinante de uma matriz usando Decomposição LU.
Um caso especial de complexidade polinomial é a complexidade quadrática, na qual c = 2. - Complexidade fatorial O(n!).
Uma das piores complexidades em termos de custo. O tempo necessário para execução do algoritmo cresce astronomicamente conforme aumenta a quantidade de dados de entrada.
Exemplo: Encontrar o determinante de uma matriz usando o Teorema de Laplace
Alterar a complexidade de um algoritmo, por exemplo de linear para logarítmica, pode fazer com que a aplicação tenha uma performance milhões ou até bilhões de vezes maior.
O gráfico a seguir mostra uma comparação entre diversos níveis de complexidade, relacionando o número de operações necessárias para realizar uma tarefa de acordo com a quantidade de elementos de um conjunto de dados:
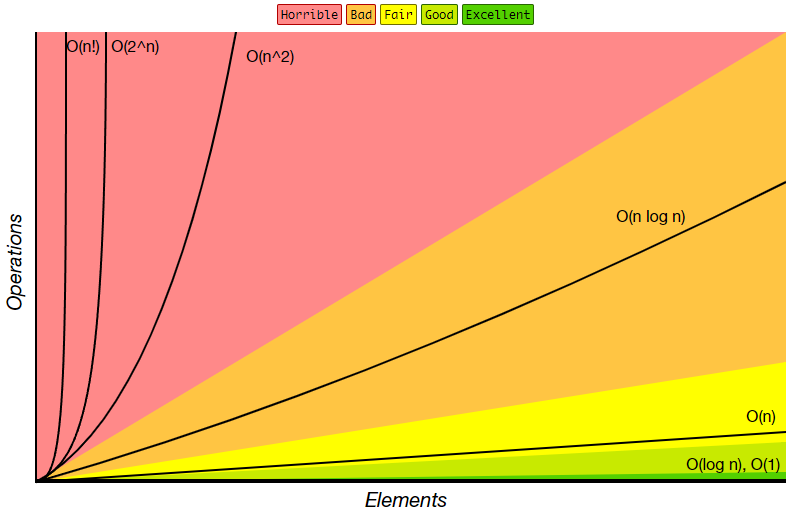
Crescimento da Complexidade de Algoritmos.
Fonte: https://www.bigocheatsheet.com/
Comparação de algoritmos com Big O distintos
Imagine que um algoritmo de busca linear de O(n) demore 1 ms (um milissegundo) para realizar uma operação, ao passo que um algoritmo de busca binária d O(log n) também demora 1 ms para realizar a operação.
Quantas operações serão necessárias para realizar n operações com cada algoritmo? A tabela a seguir mostra alguns valores calculados:
| Núm. de Elementos no Conjunto |
Busca Linear: O(n) | Busca Binária: O(log n) |
| 10 | 10 ms | 3 ms |
| 100 | 100 ms | 7 ms |
| 10.000 | 10 s | 14 ms |
| 1.000.000.000 | 11 dias | 32 ms |
Perceba que o algoritmo de busca linear tem um aumento de custo computacional muito mais elevado do que o algoritmo de busca binária considerado.
Para conjuntos com poucos elementos a diferença entre eles é pequena, porém conforme aumentamos a quantidade de dados de entrada os algoritmos começam a se comportar de forma muito diversa.
No exemplo, para conjuntos pequenos de dados praticamente não há diferença entre usar um algoritmo ou outro, mas para conjuntos grandes o emprego do algoritmo de complexidade O(log n) é imprescindível.
Em suma, o tempo de execução para cada algoritmo não cresce na mesma proporção. Por isso é importante saber o Big O de cada algoritmo – assim é possível escolher o melhor a usar em cada caso.
A tabela a seguir mostra alguns algoritmos populares de ordenação de arrays (vetores), com suas complexidades de tempo e espaço na notação Big-O:
| Algoritmo | Complexidade temporal | Complexidade espacial |
| Selection Sort | O(n2) | O(1) |
| Insertion Sort | O(n2) | O(1) |
| Bubble Sort | O(n2) | O(1) |
| Heapsort | O(n log n) | O(1) |
| Mergesort | O(n log n) | O(n) |
| Quicksort | O(n2) | O(log n) |
| Tree Sort | O(n2) | O(n) |
Outras Notações de Complexidade Algorítmica
Além do Big O, existem outras notações que podem ser empregadas para determinar o custo computacional de algoritmos, geralmente se focando em fatores distintos. Algumas delas são:
- Notação Omega (Ω()): descreve o limite inferior da complexidade
- Notação Theta (Θ()): descreve o limite exato da complexidade
- Notação Little O (o()): descreve o limite superior, porém excluindo o limite exato.
Resumo
- Conhecendo o Big O de um algoritmo, saberemos qual a performance e eficiência de acordo com o volume de informações que entram.
- Quando comparamos algoritmos distintos que resolvem o mesmo problema, por meio do Big O podemos determinar qual deles é o mais eficiente.
- De forma bem simplificada, o Big O nos diz quantas operações um algoritmo precisa realizar para completar sua tarefa.
Referências
- Erickson, J. Algorithms. 1ª edição, 2019. Disponível para download em http://jeffe.cs.illinois.edu/teaching/algorithms/
- Sedgewick, R.; Wayne, K. Algorithms. 4 edição, 2011. Editora Addison-Wesley Professional.
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L. Introduction to Algorithms. 3ª edição, 2009. Editora MIT Press.





Escreva um comentário