Teoremas de De Morgan – Eletrônica Digital
Teoremas de De Morgan
Utilizamos os Teoremas de De Morgan para realizar a simplificação de expressões booleanas e também no desenvolvimento de circuitos digitais diversos. Eles foram propostos pelo matemático britânico Augustus De Morgan, no século XIX.
Os Teoremas
Há dois teoremas, conforme segue:
1º Teorema de De Morgan
Teorema do Complemento do Produto. Esse teorema diz que o complemento do produto é igual à soma dos complementos, ou seja:
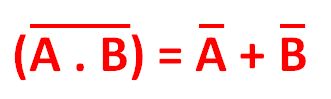
A fórmula mostra o teorema sendo aplicado a duas variáveis de entrada, mas ele pode ser estendido para mais variáveis, quantas forem necessárias.
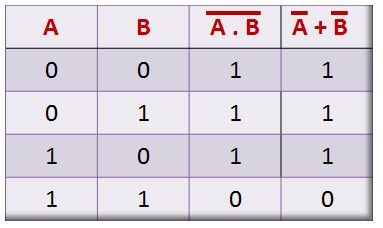
A tabela-verdade a seguir mostra o teorema sendo aplicado e a igualdade entre os membros é provada:
2º Teorema de De Morgan
Teorema do complemento da soma. Esse teorema diz que o complemento da soma é igual ao produto dos complementos, sendo uma extensão do complemento estudado anteriormente:
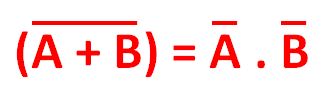
Da mesma forma que com o primeiro teorema, a fórmula mostra sua aplicação a duas variáveis de entrada, mas ele pode ser estendido para mais variáveis, quantas forem necessárias.
A tabela-verdade a seguir mostra o teorema sendo aplicado e a igualdade entre os membros sendo provada:
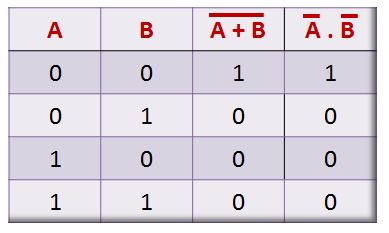
Com esses dois teoremas podemos simplificar grandemente a resolução de circuitos digitais, sendo uma ferramenta indispensável para o estudo de Eletrônica Digital.
Exemplos
(Retirados do livro “Sistemas Digitais, Princípios e Aplicações“, de Tocci & Widmer)
1 – Simplifique a expressão booleana abaixo:

2 – Simplifique a expressão a seguir usando os teoremas de De Morgan:

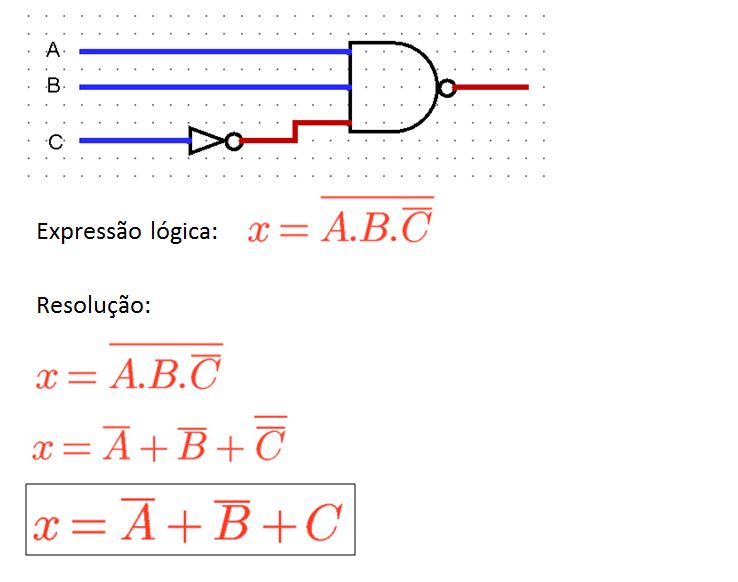
3 – Descubra a expressão lógica para a saída do circuito abaixo e simplifique-a com os Teoremas de De Morgan:





boa tarde.
gostaria de fazer o curso de eletrônica.
valeu
Segundo o teorema de Morgan, sendo os circuitos lógicos duais, para cada operação existe o seu complemento. Assim, o mesmo resultado pode ser obtido para uma expressão complementar invertendo-se todas as funções lógicas. Dessa forma, o complemento do produto é igual à soma dos complementos, e também o complemento das somas deve ser igual ao complemento dos produtos.
Suponha que, durante uma aula, ao simplificar uma equação, você encontrou a seguinte expressão:
S=(Ā.B+C)‾