Tweet

Adição Binária

Podemos efetuar operações aritméticas com valores em binário, sendo a operação mais comum a Adição Binária (soma de bits). A tabela a seguir mostra os resultados possíveis em uma soma de dois bits (bit A e bit B), incluindo além da soma em si o bit de Carry (“vai-um”). O carry indica se devemos somar 1 à próxima coluna à esquerda durante o cálculo:

Entradas		Saídas
A	B	Soma	Carry
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Note que sempre que um dos valores a serem somados for igual a zero, o resultado é trivial, como em uma soma algébrica comum. Porém, quando os dois bits são iguais a 1, o resultado será igual a zero e teremos um bit de carry gerado. Ou seja, a soma 1 + 1 é igual a 0 e “vai um”, que é a soma do valor 1 à segunda casa binária, à esquerda da casa que contém os bits somados:

+ 1

1

10

A próxima tabela mostra os resultados possíveis quando o carry de uma coluna anterior (chamado de carry-in) é adicionado às entradas A e B. Teremos como resultados a soma S e um valor chamado carry-out (vai-um-saída):

Entradas			Saídas
Carry-in	A	B	S	Carry-out
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Por exemplo, ao somarmos os bits 1 + 1 com um carry de 1, teremos como resultado o valor 1 e um carry-out gerado (outro bit 1 – “vai-um”), que será transportado para a próxima casa binária à esquerda, transformando-se em um carry-in (a ser somado).

Com o auxílio dessa tabela, vamos resolver alguns exemplos de adição binária:

1 – Efetuar: 11110₂ + 1100₂

Resolução:

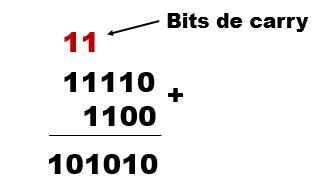
Resposta: 101010₂

2 – Somar: 1110010₂ + 1001110₂

Resolução:

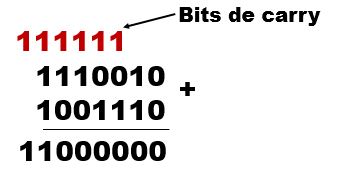
Resposta: 11000000₂

3 – Efetuar: 1011₂ + 101₂ + 1001₂

Resolução:

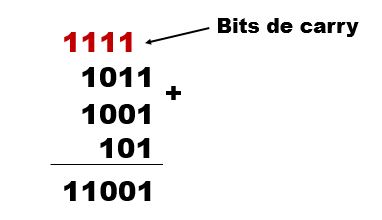
Resposta: 11001₂

É isso aí! A adição binária é uma operação muito comum, mas não é a única. Na próxima lição vamos estudar a Subtração Binária.