Medidas de Tendência Central: Média, Moda e Mediana em Python
Como calcular Média, Moda e Mediana em Python
A linguagem Python possui uma série de bibliotecas para cálculo estatístico que encontram inúmeras aplicações nas áreas de Inteligência Artificial, Ciência de Dados, Machine Learning (Aprendizado de Máquina), Big Data e muitas outras, sendo muito empregadas por quem trabalha nos ramos financeiro, médico, de engenharia e outros.
Estatística Descritiva
Chamamos de Estatística Descritiva ao ramo da matemática que nos permite descrever e sumarizar dados numericamente. Além disso, também é possível ilustrar os dados por meio do emprego de gráficos, histogramas e plotagens diversas.
Tipos de Medidas Estatísticas
Existem vários tipos de medidas estatísticas, sendo que as mais comuns são:
- Medidas de Tendência Central
- Medidas de Dispersão (Variabilidade)
- Medidas de Correlação
Neste tutorial você aprenderá a usar funções para cálculos de medidas de tendência central em Python.
População
Em Estatística, chamamos de População ao conjunto de todos os elementos que nos interessam em uma análise. Porém, é muito comum que as populações sejam conjuntos de dados muito grandes, tornado-se difícil trabalhar com a coleta e análise desses dados.
Por conta disso, é muito comum trabalhar com um subconjunto representativo de uma população, que chamamos de Amostra, a qual preserva as características estatísticas da população de modo a poder representá-la, com uma quantidade menor de dados.
Medidas de Tendência Central
As Medidas de Tendência Central em Estatística mostram os valores centrais de um conjunto de dados (população). Vamos trabalhar com as seguintes medidas de tendência central em Python nesta lição:
- Média Aritmética
- Média Harmônica
- Mediana
- Moda
Bibliotecas Estatísticas em Python
Em Python temos diversas bibliotecas para cálculo estatístico, e faremos uso neste tutorial das seguintes, que são as mais empregadas atualmente:
- statistics – Biblioteca embutida (built-in) usada para estatística descritiva.
- NumPy – Biblioteca de terceiros usada para computação numérica, altamente otimizada para o trabalho com arrays de uma ou múltiplas dimensões. Possui várias funções para análise estatística.
- SciPy – Outra biblioteca de terceiros, usada em Computação Científica, baseada na biblioteca NumPy. Acrescenta funcionalidade ao NumPy, incluindo funções estatísticas de análise.
- Matplotlib – Biblioteca de terceiros usada para visualização de dados. Pode trabalhar em conjunto com as biblitecas estatísticas citadas.
Importante: Você precisa ter as bibliotecas Scipy e Numpy instaladas para poder executar diversos métodos apresentados aqui. Caso não as tenha, abra um prompt de comandos (no Windows) e execute os comandos a seguir:
python -m pip install pip3 install scipy
Estes comandos devem instalar as duas bibliotecas necessárias. Se estiver usando Linux (Debian, Ubuntu, etc.), rode:
sudo apt install python3-pip sudo pip3 install scipy
Imports
Vamos precisar importar os módulos Scipy e Numpy para podermos executar algumas das funções estatísticas, além do módulo Math para efetuar alguns cálculos matemáticos (fórmulas). Também trabalharemos com o módulo padrão statistics. Para importar os módulos necessários, use as seguintes declarações:
import statistics import math from scipy import stats import numpy from collections import Counter
Lista de valores
Vamos trabalhar com listas de valores numéricos e de strings para estudar as funções estatísticas. Essas listas serão nossas amostras. Para criar as listas, usaremos as instruções a seguir:
lista = [2,5,7,4,1,9,5,9,2,6,7,9,4,3,5,7] listaFrutas = ['banana','laranja','maçã','abacate','laranja','melão']
Assim criamos duas listas: uma de números e outra com nomes de frutas (string).
Média Aritmética em Python
Média aritmética, ou simplesmente Média, é simplesmente a soma de todos os valores em uma amostra, dividida pela quantidade de itens somados. Por exemplo, a média aritmética dos valores do conjunto {10, 20, 30, 20} é igual a (10 + 20 + 30 + 20) / 4 = 80 / 4 = 20.
Em Python, podemos usar a função statistics.mean(lista) para calcular a média aritmética dos valores presentes em uma lista. Vejamos um exemplo:
media = statistics.mean(lista)
print("Média aritmética: ", media)
Resultado:
Média aritmética: 5.3125
Média Harmônica em Python
A Média Harmônica é um tipo especial de média, usada sempre que a série de dados apresentar uma relação inversa entre os dados, por exemplo quando precisamos calcular a velocidade média, pois conforme a velocidade aumenta, o tempo relacionado diminui.
Equivale ao inverso da média aritmética, porém com os dados invertidos. A fórmula a seguir pode ser usada para calcular a média harmônica H matematicamente:
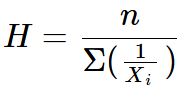
Em Python, podemos usar a função statistics.harmonic_mean(lista) para calcular a média harmônica dos valores presentes em uma lista. Vejamos um exemplo:
mediaHarmonica = statistics.harmonic_mean(lista)
print("Média harmônica: ", mediaHarmonica)
Resultado:
Média harmônica: 3.66812227074235
Mediana em Python
Em Python, podemos usar a função statistics.median(lista) para calcular a mediana dos valores presentes em uma lista. Vejamos um exemplo:
mediana = statistics.median(lista)
print("Mediana: ", mediana)
Resultado:
Mediana: 5.0
Moda em Python
Suponha a seguinte lista de items:
listaItens = ["SP", "RJ","MG","SP","TO","RS","SC","SP","SC"]
Qual valor aparece mais vezes na lista? Podemos descobri-lo determinando a moda do conjunto de valores, como segue:
moda = statistics.mode(listaItens) print(moda)
Resultado
SP
Também podemos descobrir a moda do conjunto de valores com a função stats.mode(), do módulo Scipy, como segue:
moda = stats.mode(listaItens) print(moda)
Resultado:
ModeResult(mode=array(['SP'], dtype='<U2'), count=array([3]))
Este exemplo retornou uma distribuição monomodal. O que acontece se nosso conjunto de valores possuir mais de uma moda? Vamos testar com nossa lista original:
lista = [2,5,7,4,1,9,5,9,2,6,7,9,4,3,5,7] moda = statistics.mode(lista) print(moda)
Resultado:
5
Note que apenas um valor foi retornado, porém em nosso conjunto de valores existem 3 números que aparecem com mais frequência: 5, 7 e 9, todos aparecendo três vezes. Assim, a função statistics.mode() retornou apenas o primeiro valor do conjunto multimodal. Para que seja possível retornar todos os valores de moda, devemos usar a função statistics.multimode(), com segue:
lista = [2,5,7,4,1,9,5,9,2,6,7,9,4,3,5,7] moda = statistics.multimode(lista) print(moda)
Resultado
[5, 7, 9]
A função retornou uma lista de valores com as modas obtidas. Note que a função statistics.multimode somente está disponível no Python a partir de sua versão 3.8.
Contar Ocorrências de Valores em uma Lista
Podemos contar o número de ocorrências de cada valor em uma lista usando a função Counter(lista):
print(Counter(lista)) #contar ocorrências de valores em uma lista
Resultado:
Counter({5: 3, 7: 3, 9: 3, 2: 2, 4: 2, 1: 1, 6: 1, 3: 1})
Note que não se trata da contagem de quantos itens uma lista possui, mas sim a quantidade de cada item armazenado na lista. O cálculo de ocorrências é útil para a criação de algoritmos que, por exemplo, calculem a moda de uma população, sem a necessidade de empregar funções pré-existentes – às vezes, não é possível importar determinadas bibliotecas e, quando isso ocorre, é necessário escrever um algoritmo próprio. Veremos como fazer isso em outra lição.
No próximo tutorial continuaremos a estudar Estatística Descritiva com Python, abordando as medidas de dispersão, que incluem o cálculo de Variância e Desvio-Padrão.




Escreva um comentário