Tweet

Estatística – Variância e Desvio-Padrão

Dispersão

Usamos o termo dispersão para indicar o grau de afastamento de um grupo de valores em relação à sua média aritmética (do conjunto).

Amplitude

Definimos a amplitude como sendo a diferença entre o maior e o menor valor em um intervalo de valores. Por exemplo, se tivermos um conjunto de valores ordenados, no qual o menor valor é 15 e o maior valor é 45, teremos uma amplitude de 45 – 15 = 30.

Essa amplitude nos dá uma noção do quão afastados estão o maior e o menor valores, porém não nos traz informações sobre os demais elementos do conjunto de dados.

Intervalo Interquartil

A amplitude geralmente é afetada quando existem valores muito grandes ou muito pequenos presentes no intervalo. Podemos diminuir o impacto desse problema usando o intervalo interquartil, que se obtém ignorando-se os quartis superior e inferior dos dados. Um quartil equivale a 1/4 dos valores, ou 25%.

Podemos calcular o intervalo interquartil usando o método a seguir:

1. Primeiramente, coloque os dados em ordem (crescente).
2. Determine o valor onde 1/4 dos demais valores estejam abaixo dele – chamamos esse valor de primeiro quartil (ou ainda, 25º percentil).
3. Encontre o valor onde 3/4 dos demais valores estejam abaixo dele – chamamos a esse valor de terceiro quartil (ou ainda, 75º percentil).
4. Agora calcule a diferença entre esses valores.

Exemplo: Seja o conjunto de valores a seguir (já ordenados):

1 3 4 6 7 8 10 15 16 17 18 20 21 22 25 28

Dividimos o intervalo em quatro partes:

1 3 4 6

7 8 10 15

16 17 18 20

21 22 25 28

Temos então que o primeiro quartil é o número 7, e o terceiro quartil é o número 21. O intervalo interquartil é a amplitude entre esses dois valores, portanto é igual a 21 – 7 = 14.

Desvio Médio Absoluto

É uma medida de dispersão que leva em consideração todos os valores de dados considerados. Basicamente, o desvio médio absoluto nos diz o quão afastado da média cada valor está.

Calculamos o desvio médio absoluto com a fórmula a seguir:

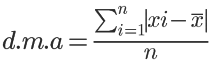
ou seja, subtraímos a média de cada valor individual, usando o valor absoluto de cada diferença, somando-os e dividindo o resultado pelo número de valores utilizados.

Exemplo: Calcular o desvio médio absoluto do conjunto de dados a seguir:

22 23 20 24 26 24 29

Vamos ordenar os sete valores e calcular a distância de cada um em relação à média do conjunto, que é 24:

Valor	Distância da média (em módulo)
20	|20 – 24| = 4
22	|22 – 24| = 2
23	|23 – 24| = 1
24	|24 – 24| = 0
24	|24 – 24| = 0
26	|26 – 24| = 2
29	|29 – 24| = 5

Aplicando a fórmula do desvio médio absoluto temos:

 

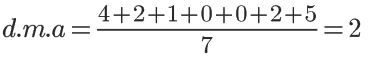
Variância

Geralmente elevamos ao quadrado cada valor de desvio e calculamos o valor médio desses quadrados, em vez de usar simplesmente o desvio médio absoluto como medida de dispersão. Damos a essa medida o nome de variância.

Simbolizamos a variância como σ² (sigma ao quadrado), e a fórmula para o cálculo da variância é a seguinte:

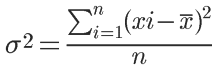
Essa fórmula é bem parecida com a fórmula do desvio médio absoluto, mas usando os quadrados dos números em vez de seus valores absolutos.

Exemplo: Vamos calcular a variância do exemplo utilizado anteriormente, no tópico sobre desvio médio absoluto:

Valor	Distância da média	Distância média ao quadrado
20	-4	16
22	-2	4
23	-1	1
24	0	0
24	0	0
26	2	4
29	5	25

Calculando a variância:

 

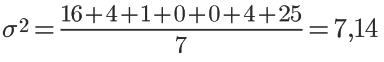
Desvio-Padrão

No geral, usamos uma medida de dispersão chamada de Desvio-Padrão, que dá uma idéia mais clara do tamanho da dispersão dos dados. O desvio-padrão nada mais é do que a raiz quadrada da variância. Assim:

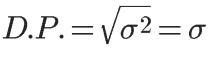
O símbolo do desvio-padrão é a letra grega sigma (σ).

Exemplo: Aplicando o cálculo do desvio-padrão ao nosso exemplo anterior, teremos:

que é um valor de dispersão mais claro que a variância e mais preciso que o desvio médio absoluto.

Coeficiente de variação

Podemos verificar se a dispersão é muito grande em relação à média, calculando o Coeficiente de Variação, que é a razão entre o desvio-padrão e a média:

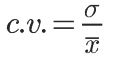
Aplicando-se essa fórmula ao exemplo usado no artigo:

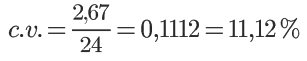
Portanto o coeficiente de variação do conjunto de dados apresentado é de 11,12%.