Tópicos em Matemática – Média, Mediana e Moda – Estatística
Tópicos em Matemática – Média, Mediana e Moda
Estatística Descritiva – Medidas de Tendência Central
As médias são valores representativos de um conjunto de dados. Esses valores possuem a tendência de se localizarem em um ponto central, dentro do conjunto de dados, e por isso as médias são chamadas de Medidas de Tendência Central.
Existem vários tipos de médias que podem ser calculadas, sendo as mais comuns a média aritmética (ou somente média), a mediana, a moda, a média geométrica e a média harmônica. Cada uma delas tem suas aplicações específicas, vantagens e desvantagens de uso. Nesta lição trataremos dos três primeiros tipos: Média (aritmética), Moda e Mediana.
Média (ou Média Aritmética)
Indicada por ![]() (“x barra”), pode ser calculada como:
(“x barra”), pode ser calculada como:
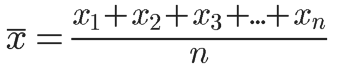
Onde x1, x2, etc, são os números para os quais queremos calcular a média. Podemos também usar a notação de somatório para representar o valor médio:
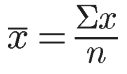
O que significa “a média é igual ao somatório dos números sobre n”. Já o somatório de x é dado por:
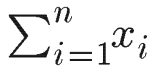
O que significa “somatório dos números de x1 até xn“.
Exemplo: Dado o conjunto de notas a seguir, calcule a média da disciplina para um aluno do curso de Matemática:
| Disciplina | Nota 01 | Nota 02 | Nota 03 | Nota 04 |
| Matemática | 8 | 7,4 | 6,2 | 8,8 |
A média das quatro notas será dada por:
Média = (8 + 7,4 + 6,2 + 8,8) / 4 = 30,4 / 4 = 7,6
Mediana
Trata-se do ponto (ou elemento) a meio caminho na escala de dados, ou seja, metade dos valores está acima da mediana e a outra metade está abaixo.
Para calcular a mediana, devemos primeiramente ordenar a lista de números considerados (rol). Por exemplo, seja a lista de valores numéricos a seguir:
20 35 19 24 55 18 17 20 23
Ordenando essa lista, teremos:
17 18 19 20 20 23 24 35 55
A mediana desse conjunto de valores é 20, pois há quatro números abaixo e quatro números acime desse valor que, portanto, é o ponto central.
Se tivermos um número par de valores, poderemos descobrir a mediana calculando a média entre os dois números centrais. Por exemplo, no conjunto de valores a seguir:
17 19 20 22 27 29
os dois números centrais são 20 e 22. A mediana será então (20 +22) / 2 = 21.
Quando uma relação de valores contém um número muito afastado dos outros da lista, a média não é uma medida muito representativa. Veja o exemplo a seguir, onde temos listados os valores dos salários dos funcionários de uma empresa, de acordo com o cargo:
| Cargo | Salário |
| Técnico | R$ 2000,00 |
| Analista | R$ 2300,00 |
| Auxiliar adm. | R$ 1900,00 |
| Publicitário | R$ 2100,00 |
| Presidente | R$ 11500,00 |
O valor médio dos salários dessa empresa será 19800 / 5 = R$ 3960,00. Porém, note que todos os funcionários, à exceção do presidente, recebem bem menos do que isso – cerca da metade do valor médio. Portanto, a média aritmética não mostra com clareza o que ocorre nesse caso.
Para termos uma idéia melhor dos salários pagos pela empresa, podemos usar então a mediana. Vamos ordenar a lista de salários e descobrir sua mediana:
1900 2000 2100 2300 11500
A mediana (valor central) é R$ 2100,00, sendo essa uma medida de tendência central bem melhor, nesse caso.
A mediana é, em essência, a média aritmética dos valores centrais do rol considerado.
Moda
A moda é o valor que ocorre com maior frequência em um conjunto de valores (valor mais comum). Se houver mais de um valor nessa condição, chamamos a todos eles de modas. Uma distribuição com duas modas é chamada de bimodal. Já a distribuição que possui apenas uma única moda é denominada unimodal.
Exemplo: Dado o conjunto de valores a seguir, descubra sua moda:
17 18 19 20 20 23 24 35 55
A moda nesse exemplo é o número 20, pois esse valor aparece duas vezes no conjunto.
Quando nenhum valor ocorre mais de uma vez, não existe a moda para o conjunto considerado.
É isso aí! Vimos nesse artigo algumas medidas de tendência central, e na próxima lição estudaremos as medidas de dispersão, como o Desvio Padrão. Até mais!





Escreva um comentário