Algoritmo Torre de Hanoi em Python
Torre de Hanoi
A Torre de Hanoi é um famoso quebra-cabeça ou problema matemático, inventado pelo matemático francês François Édouard Anatole Lucas no século XIX, que consiste em mover uma pilha de discos de tamanhos diferentes de uma haste de origem para uma haste de destino, usando uma haste intermediária. A regra básica é que um disco maior nunca pode ficar em cima de um disco menor.
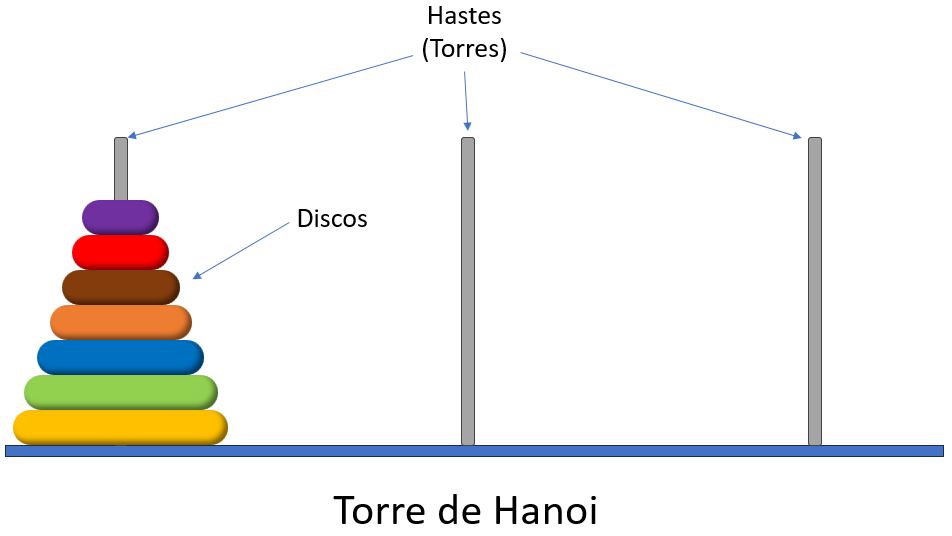
Torre de Hanoi com sete discos e três hastes
A configuração inicial consiste em três hastes (podemos chamá-las de A, B e C) e uma pilha de discos de tamanhos diferentes posicionados em ordem decrescente em uma das hastes (geralmente a haste A). O objetivo é mover todos os discos da haste A para a haste C, utilizando a haste B como intermediária, seguindo as seguintes regras:
1. Apenas um disco pode ser movido por vez.
2. Um disco só pode ser movido se estiver no topo da pilha em sua haste atual.
3. Um disco maior nunca pode ficar em cima de um disco menor.
O desafio é encontrar a sequência correta de movimentos para transferir todos os discos da haste A para a haste C. A solução ótima para a Torre de Hanoi requer 2n – 1 movimentos, onde n é o número de discos.
Ou seja, com 3 discos é possível resolver a torre em 23 – 1 = 7 movimentos. Já uma torre com 7 discos necessitará de 27 – 1 = 127 movimentos.
A Torre de Hanoi é um problema clássico de recursão e tem aplicações em algoritmos, programação e teoria da computação para ilustrar conceitos como recursão, pilha de chamadas e complexidade algorítmica.
Algoritmo da Torre de Hanoi
Vejamos um exemplo de algoritmo em Python que resolve uma Torre de Hanoi, recebendo como entrada do usuário o número de discos desejado. Vamos usar uma abordagem recursiva neste exemplo.
Chamaremos as hastes (torres) de A, B e C para identificação ao chamar a função no programa principal, como mostra a figura a seguir:
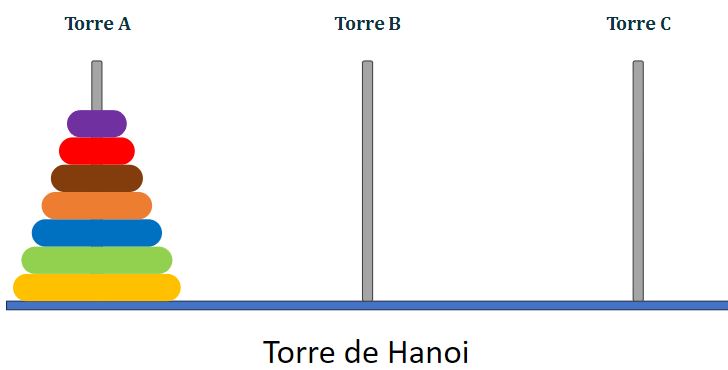
Hastes das Torres de Hanoi
O objetivo é mover todos os discos da torre A para a torre C. Vamos ao código agora.
def torre_hanoi(n, origem, destino, auxiliar):
if n == 1:
print(f"Mova o disco 1 de {origem} para {destino}")
return
torre_hanoi(n-1, origem, auxiliar, destino)
print(f"Mova o disco {n} de {origem} para {destino}")
torre_hanoi(n-1, auxiliar, destino, origem)
if __name__=='__main__':
# Exemplo de uso
n = int(input("Digite o número de discos: "))
torre_hanoi(n, "A", "C", "B")
Testando:
Digite o número de discos: 3 Mova o disco 1 de A para C Mova o disco 2 de A para B Mova o disco 1 de C para B Mova o disco 3 de A para C Mova o disco 1 de B para A Mova o disco 2 de B para C Mova o disco 1 de A para C
Funcionamento
Nesse algoritmo, a função torre_hanoi() recebe quatro parâmetros: o número de discos n, a torre de origem origem, a torre de destino destino e a torre auxiliar auxiliar. A função utiliza a recursão para resolver o problema da Torre de Hanoi.
Quando há apenas um disco, ele é movido diretamente da torre de origem para a torre de destino. Caso contrário, a função chama recursivamente a si mesma para mover n-1 discos da torre de origem para a torre auxiliar, em seguida move o disco restante da torre de origem para a torre de destino e, por fim, move os n-1 discos da torre auxiliar para a torre de destino.
O algoritmo exibe as instruções para mover cada disco, indicando de qual torre para qual torre ele deve ser movido. Basta executar o algoritmo informando o número de discos desejado para ver a solução para a Torre de Hanoi.
Modificação do algoritmo
Vamos modificar o algoritmo anterior para que ele mostre também o número de movimentos realizados para resolver a torre:
def torre_hanoi(n, origem, destino, auxiliar):
if n == 1:
print(f"Mova o disco 1 de {origem} para {destino}")
return 1
movimentos = torre_hanoi(n-1, origem, auxiliar, destino)
print(f"Mova o disco {n} de {origem} para {destino}")
movimentos += 1
movimentos += torre_hanoi(n-1, auxiliar, destino, origem)
return movimentos
if __name__=='__main__':
# Exemplo de uso
n = int(input("Digite o número de discos: "))
total_movimentos = torre_hanoi(n, "A", "C", "B")
print(f"Total de movimentos realizados: {total_movimentos}")
Testando:
Digite o número de discos: 3 Mova o disco 1 de A para C Mova o disco 2 de A para B Mova o disco 1 de C para B Mova o disco 3 de A para C Mova o disco 1 de B para A Mova o disco 2 de B para C Mova o disco 1 de A para C Total de movimentos realizados: 7
Funcionamento
1. Definimos a função torre_hanoi, que recebe como parâmetros o número de discos n, os nomes das torres origem, destino e auxiliar.
2. Dentro da função, verificamos se n é igual a 1. Se sim, significa que temos apenas um disco a ser movido, então imprimimos a instrução para mover o disco da origem para o destino e retornamos 1, indicando que foi realizado um movimento.
3. Caso contrário, temos mais de um disco. Chamamos recursivamente a função torre_hanoi para mover n-1 discos da origem para a auxiliar, usando o destino como torre auxiliar. Armazenamos o número de movimentos retornados em movimentos.
4. Imprimimos a instrução para mover o disco n da origem para o destino e incrementamos movimentos em 1, já que realizamos mais um movimento.
5. Chamamos novamente recursivamente a função torre_hanoi para mover os n-1 discos restantes da auxiliar para o destino, usando a origem como torre auxiliar. Somamos o número de movimentos retornados ao total de movimentos atual.
6. Retornamos o total de movimentos realizados.
7. No exemplo de uso, solicitamos ao usuário que digite o número de discos desejado.
8. Chamamos a função torre_hanoi passando o número de discos, os nomes das torres “A”, “C” e “B” como argumentos, respectivamente. Armazenamos o total de movimentos retornados em total_movimentos.
9. Por fim, exibimos o total de movimentos realizados na solução.
Conclusão
Concluindo, vimos que a Torre de Hanoi é um enigma matemático fascinante que desafia a mente e tem sido objeto de estudo e entretenimento há muito tempo.
Por meio dos exemplos de algoritmos em Python, ficou claro que a solução para o que aparenta ser um quebra-cabeça complexo é surpreendentemente elegante e simples. Com a implementação da função recursiva (pode ser feito de forma iterativa também), pudemos observar uma abordagem para a resolução da Torre de Hanoi, perfeita para o estudo de recursividade em algoritmos e lógica de programação.
Além de ser uma demonstração de habilidades de programação e lógica, o estudo da Torre de Hanoi oferece insights valiosos para a computação e outras áreas da matemática. Como vimos, é um excelente exercício para compreender a recursividade e a otimização de algoritmos.
Colabore com a Bóson Treinamentos
Ajude o canal adquirindo meus cursos na Udemy:
- Bancos de Dados com MySQL Básico: https://bit.ly/35QdWE4
- Lógica de Programação com Português Estruturado: https://bit.ly/3QKPn22
- Programação em Python do Zero: https://bit.ly/python-boson
Adquira também livros e outros itens na loja da Bóson Treinamentos na Amazon e ajude o canal a se manter e crescer: https://www.amazon.com.br/shop/bosontreinamentos





Muito interessante. Um programador pleno, por exemplo, deveria ser capaz de montar tal algoritmo sem a necessidade de consultar esse post ou é considerado algo não trivial para todos os níveis de experiência?
Um programador experiente deveria ser capaz de criar um algoritmo desse tipo (não necessariamente idêntico) sem consultas, apenas aplicando princípios de lógica de programação, estruturas de dados e sintaxe da linguagem de programação empregada.
Bom dia. Me chamo Mauricio. Eu li um artigo sobre Numeros Primos no seu site. Estou com dificuldade para localizar aqui. Pode me dizer a data em que ele foi postado…
Obrigado.
Bom dia Maurício!
Os artigos sobre números primos que tenho aqui são os seguintes:
Números Primos em JavaScript: https://www.bosontreinamentos.com.br/programacao-em-javascript/como-gerar-numeros-primos-em-javascript/
Gerar números primos em um intervalo: https://www.bosontreinamentos.com.br/programacao-em-python/como-gerar-numeros-primos-em-python-em-um-intervalo-especificado/
Determinar se número é primo em linguagem C: https://www.bosontreinamentos.com.br/programacao-em-linguagem-c/programa-para-determinar-se-um-numero-e-primo-em-c/
Espero que ajude!
Abraço.