Tweet

Recursividade em Lógica de Programação

Recursividade (ou Recursão) é um conceito em ciência da computação que se refere à capacidade de uma função ou procedimento chamar a si mesmo de forma direta ou indireta durante a sua execução. Em outras palavras, é quando uma função é definida em termos dela mesma.

Ao utilizar a recursividade, uma função pode ser dividida em problemas menores e mais simples, resolvendo-os em etapas sucessivas até alcançar um caso base, que é uma condição que não requer chamadas recursivas e permite a conclusão do processo.

A recursividade é frequentemente usada para resolver problemas que podem ser subdivididos em subproblemas do mesmo tipo. Essa abordagem é especialmente útil quando a estrutura do problema é recursiva por natureza. Alguns exemplos de algoritmos recursivos comuns incluem a busca em árvores, a ordenação rápida (quicksort) e o cálculo do fatorial.

Uma função recursiva geralmente possui dois componentes principais:

1. Caso base: É uma condição especial que determina quando a recursão deve parar. Quando a condição do caso base é atendida, a função recursiva não faz mais chamadas a si mesma e retorna um resultado específico.
2. Caso recursivo: É o caso em que a função se chama novamente com um problema menor ou uma instância simplificada do problema original. A chamada recursiva permite que a função trabalhe em direção ao caso base, resolvendo os subproblemas até que o resultado final seja alcançado.

No entanto, é importante ter cuidado ao usar recursão, pois um uso incorreto ou ineficiente pode levar a problemas de desempenho e até mesmo a erros como estouro de pilha (stack overflow) se não houver controle adequado das chamadas recursivas.

Existem duas categorias gerais de recursividade: Recursão Direta e Recursão Indireta.

Recursão Direta

Em uma recursão direta, uma função f(A) chama a si própria diretamente – f(A) chama f(A), em um passo recursivo único.

Recursão Indireta

Já a recursividade indireta consiste em uma função f(A) que chama uma função diferente f(B), que por sua vez chama f(A) novamente, Ou seja, é um processo recursivo de dois passos, onde a função original chama outra função que por sua vez chama a função original novamente.

Vamos estudar dois exemplos populares de algoritmos recursivos para ver a recursividade em ação: Fatorial e Fibonacci

Exemplos de algoritmos recursivos

Fatorial recursivo

O fatorial de um número inteiro positivo qualquer é dado pela fórmula:

n! = n * (n-1) * (n-2) * … * 1

Por exemplo, 5! é igual a:

5! = 5 * 4 * 3 * 2 * 1 = 120

Note que o fatorial é uma sequência de operações semelhantes, multiplicações cada vez mais básicas até chegar em 1. Perfeito para a recursão!

O fatorial pode ser calculado de forma recursiva de acordo com a seguinte sequência de operações:

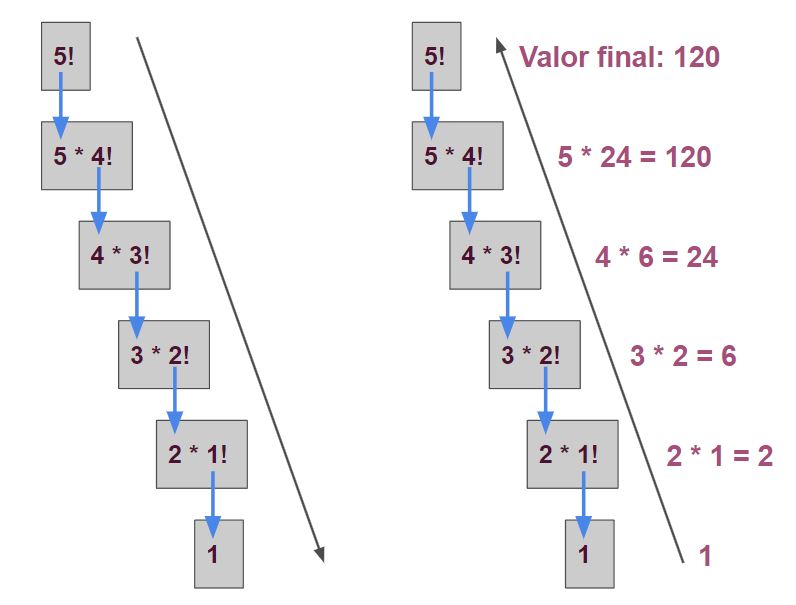
Um exemplo de código recursivo em português estruturado é a função fatorial() mostrada a seguir, que calcula o fatorial de um número inteiro passado como argumento:

// Fatorial recursivo
funcao inteiro fatorial(inteiro x) {
  se (x <= 1) {
    retorne 1
  }
  senao {
    retorne x * fatorial(x - 1)
  }
}

Esta função funciona dividindo o problema de calcular o fatorial de um número em dois subproblemas menores: calcular o fatorial de x – 1 e multiplicar o resultado por x. O subproblema de calcular o fatorial de x – 1 é resolvido por uma chamada recursiva para a própria função fatorial().

O resultado da chamada recursiva é então multiplicado por n para obter o resultado do problema original.

Fibonacci recursivo

A série de fibonacci é uma sequência numérica que inicia com 0 e 1 e onde cada número subsequente é a soma dos dois números anteriores a ele:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

Trata-se de uma série numérica que ocorre repetidamente na natureza e descreve uma forma em espiral. A razão entre dois Fibonaccis sucessivos converge para o valor 1,618…, chamado de “Proporção Áurea”, que é esteticamente muito agradável e aproveitado em várias áreas do conhecimento, como engenharia e arquitetura.

Bem, podemos definir a série de fibonacci recursivamente da seguinte forma:

fibonacci(0) = 0
fibonacci(1) = 1
fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)

Novamente uma sequência de operações semelhantes. Perfeito para a recursão!

A seguir temos um exemplo de código recursivo em português estruturado que calcula um número de Fibonacci a partir de um número inteiro x passado como argumento:

// Função fibonacci recursivo
funcao inteiro fibonacci(inteiro x) {
  se ((x == 0) ou (x == 1)) {
    retorne x
  }
  retorne fibonacci(x-1) + fibonacci(x-2)
}

Quais problemas a recursividade pode causar?

A recursividade é uma técnica de programação que pode ser útil para resolver problemas que podem ser quebrados em subproblemas menores, cada um dos quais pode ser resolvido com uma chamada recursiva. No entanto, a recursividade também pode causar alguns problemas, como:

• Escopo de variáveis: Quando uma função é chamada recursivamente, ela cria uma nova cópia de seu escopo de variáveis. Isso pode levar a problemas se as variáveis no escopo forem modificadas dentro da função.
• Eficiência: Os algoritmos recursivos podem ser muito ineficientes, especialmente para grandes problemas. Isso ocorre porque cada chamada recursiva cria uma nova pilha de chamadas. A pilha de chamadas pode crescer rapidamente e levar a problemas de memória.
• Dificuldade de depuração: Os algoritmos recursivos podem ser difíceis de depurar, pois podem ser difíceis de acompanhar o fluxo de controle da função.

É importante pesar os riscos e benefícios da recursividade antes de usá-la para resolver um problema. Em alguns casos, a recursividade pode ser a melhor solução, mas em outros casos, pode ser melhor usar uma abordagem iterativa. Se não for usada com cuidado, a recursão pode levar a programas que são lentos ou difíceis de entender.

Dicas para usar a recursividade com segurança

• Use a recursividade apenas quando necessário: Não use a recursividade apenas porque é legal. Use-a apenas quando for a melhor maneira de resolver um problema.
• Evite usar recursividade para problemas grandes: Os algoritmos recursivos podem ser muito ineficientes para problemas grandes. Se você estiver enfrentando um problema grande, considere usar uma abordagem iterativa.
• Use a recursividade com cuidado: A recursividade pode ser uma ferramenta poderosa, mas é importante usá-la com cuidado. Se não for usada com cuidado, a recursão pode levar a programas que são lentos, difíceis de entender e difíceis de depurar.

É isso aí! Nas próximas lições veremos mais técnicas de programação e algoritmos específicos que são importantes para estudantes e profissionais na área de desenvolvimento de software.

Colabore com a Bóson Treinamentos

Ajude o canal adquirindo meus cursos na Udemy:

• Bancos de Dados com MySQL Básico: https://bit.ly/35QdWE4
• Lógica de Programação com Português Estruturado: https://bit.ly/3QKPn22
• Programação em Python do Zero: https://bit.ly/python-boson

Adquira também livros e outros itens na loja da Bóson Treinamentos na Amazon e ajude o canal a se manter e crescer: https://www.amazon.com.br/shop/bosontreinamentos