Tweet

Subtração Binária com Complemento de 1

Na lição anterior aprendemos a calcular o resultado de uma subtração binária usando bits de borrow. Agora, vamos mostrar uma outra técnica para realização de subtração entre números binários, denominada Subtração com Complemento de 1, que é uma técnica utilizada pelos computadores para realizar esse tipo de cálculo.

Para humanos, a subtração usando o método do borrow é mais simples, mas certamente é de valia conhecer outros métodos também, especialmente para quem trabalha com projetos de lógica digital ou programação de computadores.

O complemento de 1 de um bit é o seu inverso (o de 1 é 0 e o de 0 é 1). Podemos usar esse complemento de 1  para efetuar uma subtração binária, de acordo com o procedimento  a seguir:

1. Iguale o número de casas binárias dos números envolvidos no cálculo, acrescentando zeros à esquerda se necessário. Obtenha o complemento de 1 do subtraendo (número que será subtraído do minuendo; “número de baixo”)
2. Some o complemento de 1 obtido no passo a) ao minuendo (número “de cima” no cálculo)
3. Se o número estourar (ultrapassar o número de casas binárias dos valores envolvidos na subtração), a resposta será um valor positivo. Somamos então o estouro ao LSB (bit menos significativo) do resultado do passo b). Chamamos essa operação de EAC (End-Around-Carry / vai-um final ao redor). Caso não haja estouro, simplesmente aplique o complemento de 1 neste resultado, e o valor obtido será um número negativo.

Vejamos um exemplo de subtração binária usando esta técnica:

Exemplo 01: Efetue o cálculo de 11001₂ – 10001₂, usando o complemento de um.

Resolução:

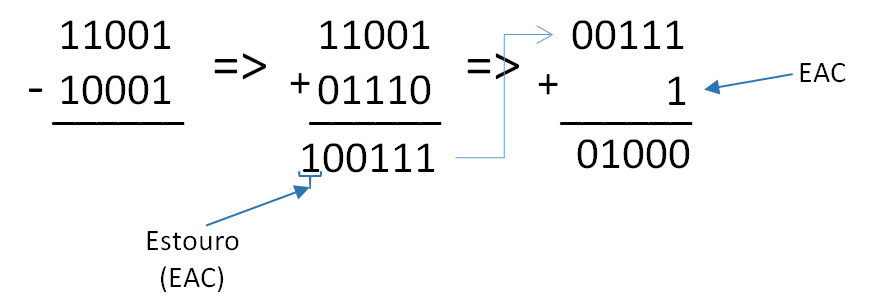
Resultado: 11001₂ – 10001₂ = 1000₂

Exemplo 02: Calcule 1011₂ – 101₂:

Resolução:

Igualamos o número de casas binárias dos números acrescentando um zero ao 101₂:

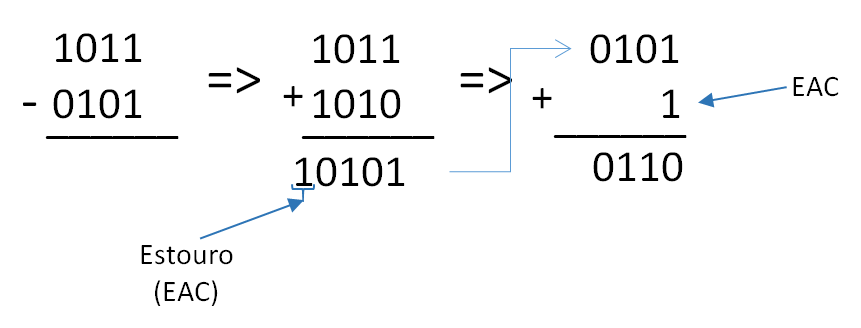
Resultado: 1011₂ – 101₂ = 110₂

Exemplo 03: Efetuar 101₂ – 11000₂ usando o complemento de um.

Resolução: Note que neste exemplo o segundo número (subtraendo) é menor do que o primeiro (minuendo) na subtração, de forma que o resultado deve ser um valor negativo.

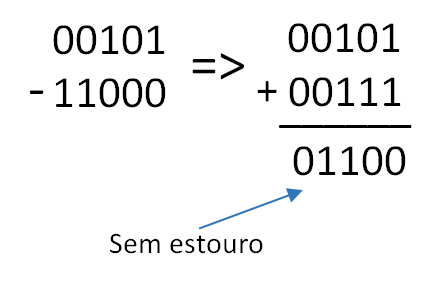
Neste caso obtivemos um número negativo. O valor real do número será dado pelo complemento de 1 do resultado anterior, incluindo o bit de estouro:

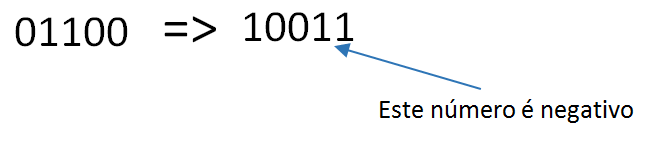
Resultado: 101₂ – 11000₂ = -10011₂ (-19₁₀)

É isso aí! Na próxima parte de nossa lição sobre subtração de números binários, vamos apresentar a subtração usando a técnica do complemento de 2.